In this section, all that concerns the definition of a view and the manipulation of a mesh will be explained.
This section presents the structure of the shot and camera of the library. After an overview of the camera model used, all the components of the shot class are listed and described. Then, a set of examples of the most important operations (projection and un-projection) and of the interactions between shots and between a shot and the trackball are presented. Finally, simple examples of a shot are visually shown, in order to help with the implementations of eventual wrapped to and from other shot-camera formats.
The camera model
In generale, the camera parameters can be divided in two groups:
If these group of values are put in a proper camera model, it is possible to transform any point in the space in the corresponding point on the image plane of the camera (and viceversa).
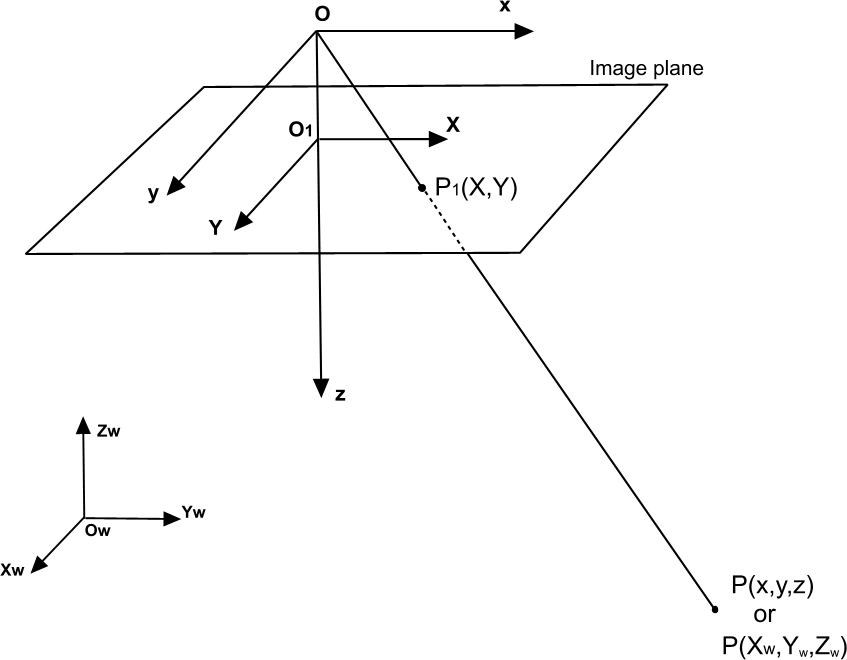
In fact, given a simple perspective camera model like the one shown in figure, extrinsic parameters can be used to transform a point from its world coordinates {xw,yw,zw} to the camera 3D coordinate system {x,y,z}):
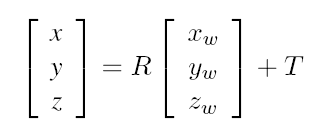
In this case the extrinsic parameters are a 3 X 3 rotation matrix R and a translation vector T, which define the orientation and position of the camera. In order to transform the 3D camera coordinate in 2D image plane coordinates (Xu,Yu) it's necessary to know the measure of the distance between the point of view and the image plane (OO1 in figure): this value, indicated with f, is usually known as the focal length. The relation between the camera and image coordinates of the point can be expressed as follows:
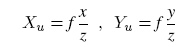
Another aspect of the structure of a camera that can be characterized is the distortion introduced by the lenses: if we suppose that the distortion is radial (performed along the radial direction respect to the center of distortion) we can calculate the undistorted image coordinates
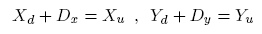
where
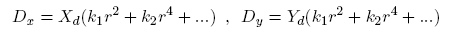
and
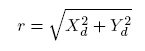
In conclusion, a quite accurate model of a camera can be described by:
While this set of parameters provides everything to transform any 3D point in its corresponding point in the image plane, this could be not enough in peculiar applications. If an accurate estimation of the real position of the camera respect to the object is needed, some more data about the camera model are needed: in particular, the sensor physical size together with the resolution in pixel of the acquired image. If these a-priori data are known, a unique set of camera parameters is associated to any shot.
The VCG Shot
The implementation of a Shot in the VCG library can be found in vcg\math\shot.h
The shot is composed by two elements:
The attributes of a Camera, which is define in vcg\math\shot.h, are:
While the extrinsic parameters usually change between the shots, some (sometimes all) of the intrinsics are strongly related to the camera model used. In particular, some values are usually known before camera calibration: viewportPx and CenterPx. Moreover, if an accurate calibration is needed, it is necessary to fill the PixelSizeMm value.
This can be inferred from the camera datasheet (it can be calculated by dividing the sensor width and height, in mm, by the resolution of the image) or, in some cases, from the EXIF of the image (in the CANON models, it is the inverse of FocalPlane X-resolution and FocalPlane Y-resolution, scaled from inches to mm if necessary). If a correct PixelSizeMm is not set, the values of the camera parameters can be different from the real ones, even though the image is perfectly aligned to a 3D model.
Also the focal distance can be inferred from EXIF, but its value is indicative. If a calibrated camera is used, then all the intrinsic parameters should be known in advance.